A Twilight Opening Night Payoff Matrix
A student was interested in seeing the new Twilight movie, Breaking Dawn Part 1. And her roommate, a “Twi-Hard,” even had an extra ticket for the opening, midnight showing. The student likes seeing the vampires and werewolves occasionally, but cannot stand the continuing screams of the mostly pre-pubescent audience. She views her situation as a game with the following payoff bi-matrix:
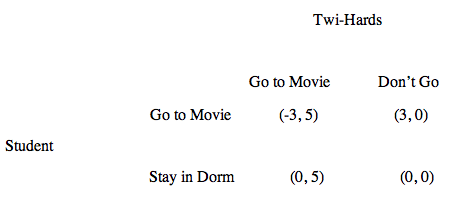
She has no dominant strategy; but understanding that the Twi-Hards do—that they will go to see Edward and Jacob on opening night no matter what, her best choice was to stay in her dorm room. (Don’t Go, Go) is a Nash Equilibrium and a Pareto optimum.
(HT to AVN)

Comments