Division, Not Long Division
Division is the most powerful arithmetic operation. It makes comparisons. When the numerator and denominator have the same units, the comparison makes a dimensionless number, the only kind that the universe cares about. Long division, however, is something else entirely. In my post “Dump algebra,” many commentators objected to my loathing of long division. But long division is not division! Long division is just one way to do the computation, and is far from the most useful way.
I’ll illustrate with an actual example of division. For my environmental-protection lawsuit, now in the Massachusetts Supreme Court, I needed to divide 142,500 by 4655. Here is the long-division calculation, my first use of the method in 30 years:

The calculation took me a few minutes with paper and pencil, some of the time to reconstruct the algorithm details and to get the bookkeeping straight — even though I already knew the answer quite accurately.
I knew the answer because I had already applied a more enjoyable method: skillful lying. I turned the numerator 142,500 into the nearby and convenient 150,000; and turned the denominator 4655 into the nearby and convenient 5000. Dividing 150,000 by 5000 gives 30. It’s likely to be an accurate estimate, because the two errors (increasing the numerator and increasing the denominator) partly compensate.
The next correction is not too hard, and comes from estimating the two errors. The actual numerator of 142,500 is 7500 less than 150,000, a decrease of 5 percent. To fix this error, decrease the estimate by 5 percent. The actual denominator of 4655 is 345 less than 5000, a decrease of, let’s say, 7 percent (7 percent of 5000 is 350). To fix this error, increase the estimate by approximately 7 percent. The two fixes together require increasing the estimate by 2 percent (7 percent minus 5 percent). So, 30 becomes 30.60—which is very close to the actual quotient of 30.6122…
This whole calculation took about 10 seconds in my head. There’s no need for long division, and I hope that I live another 30 years without using it again.
For students, learning long division mostly means learning like a parrot. A classic example is from the National Assessment of Educational Progress (NAEP) results reported in 1983 (Carpenter, T., et. al., “Results of the Third NAEP Mathematics Assessment: Secondary School,” The Mathematics Teacher, 76:652-659). Thirteen-year-olds across the country were asked:
An army bus holds 36 soldiers. If 1128 soldiers are being bused to their training site, how many buses are needed?
70 percent of the students did the long division correctly (the result of 1128/36 is 31 and 1/3). From doing the division correctly, the most popular answer, chosen by 29 percent, was the meaningless 31 R 12 (31 with a remainder of 12) buses. Another 23 percent chose 31 buses, leaving 12 soldiers stranded. Only 18 percent chose the correct answer of 32 buses. Even then it’s not clear how many of the 18 percent were sure of their answer or were just guessing between 31 and 32.
Here is a flow diagram illustrating the answer distribution:
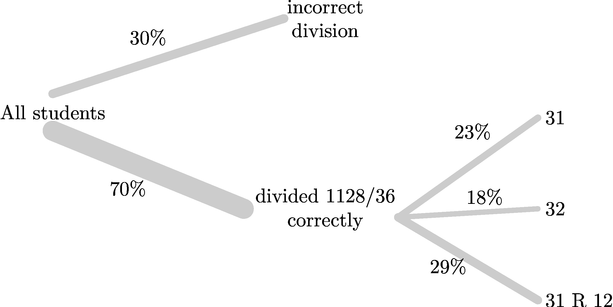
It’s easy to learn long division yet understand little.

Comments