Another Case of Teacher Cheating, or Is It Just Altruism?
From the results of the high-school “maturity exam” in Poland (courtesy of reader Artur Janc), comes this histogram showing the distribution of scores for the required Polish language test, which is the only subject that all students are required to take, and pass.
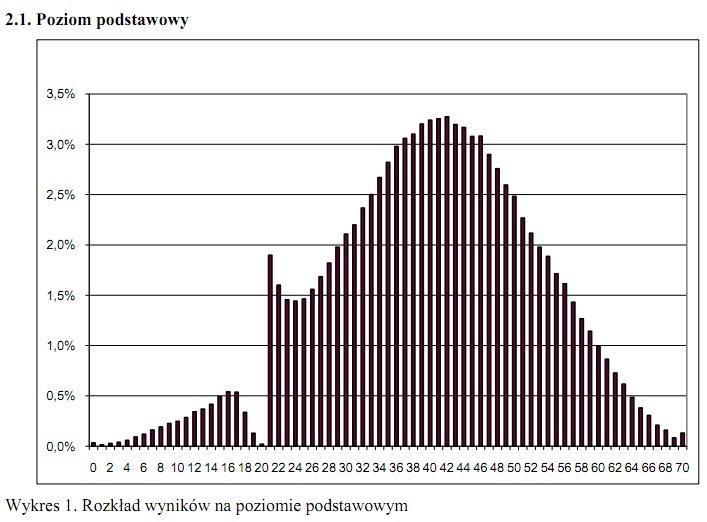
Not quite a normal distribution. The dip and spike that occurs at around 21 points just happens to coincide with the cut-off score for passing the exam. Poland employs a fairly elaborate system to avoid bias and grade inflation: removing students’ names from the exams, distributing them to thousands of teachers and graders across the country, employing a well-defined key to determine grades. But by the looks of these results, there’s clearly some sort of bias going on.
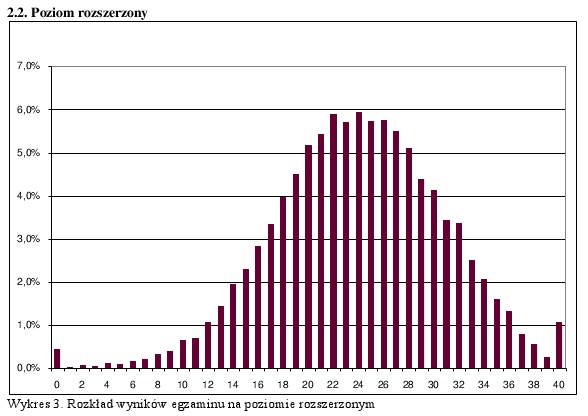
Compare that to the results of the “advanced” Polish language exam, which is taken in addition to the basic level exam by about 10% of students. It has no influence on whether students pass or fail the exit examination, so there’s no incentive to grade inflate, as evidenced by the clean distribution.
Artur writes:
I’m quite sure there is nothing to be gained for the graders/districts if they pass a student with a borderline score (at the basic level), rather than failing him/her. So my take on this is that graders just didn’t want to fail some kids and seriously hurt their college prospects and/or make them re-take the exam when the score was close to the cutoff.
So, is that pure altruism on the part of the teachers? Or do they actually have some bit of national incentive to see students go on to college? One could probably ask the same questions of school officials in Atlanta.

Comments