Addition Is Useless, Multiplication Is King: Channeling Our Inner Logarithm
TIME magazine has been running a series called “Brilliant: The science of smart” by Annie Murphy Paul. The latest column, “Why Guessing Is Undervalued,” quoted several results from research on learning estimation, a topic near to my heart. One result surprised me particularly:
…good estimators possess a clear mental number line — one in which numbers are evenly spaced, or linear, rather than a logarithmic one in which numbers crowd closer together as they get bigger. Most schoolchildren start out with the latter understanding, shedding it as they grow more experienced with numbers.
(Zoonar)
I do agree that children start out with a logarithmic understanding. I first learned this idea from a wonderful episode of WNYC’s Radio Lab on “Innate numbers” (Nov. 30, 2009). The producers had asked Stanislas Dehaene to discuss his research on innate number perception.
One of his studies involved an Indian tribe in the Amazon. This tribe does not have words for numbers beyond five, and does not have formal teaching of arithmetic. But the members have a sophisticated understanding of numbers. They were given the following problem: on a line with one object at one end, and nine objects at the other end, they were asked, “How many objects would you place directly in the middle of the line?”
What number would you choose?
Twenty years ago I would have chosen five, for five is the average of one and nine: It is larger than one by four, and smaller than nine also by four. Thus, it is halfway on a linear (or additive) number line. Almost all Western students also choose five. However, the members of the Indian tribe chose three. That choice also makes sense, but in a different way: Three is larger than one by a factor of 3, and smaller than nine also by a factor of 3. Thus, three is halfway between one and nine on a multiplicative or logarithmic number line.
Dehaene concludes, and I agree, that our innate perception of numbers is logarithmic (or multiplicative); and that we learn our linear (or additive) scale through our culture. More details are in their paper in Science, whose abstract contains this summary:
This indicates that the mapping of numbers onto space is a universal intuition and that this initial intuition of number is logarithmic. The concept of a linear number line appears to be a cultural invention that fails to develop in the absence of formal education.
So far so good. However, in the Radio Lab interview that I mentioned above, and in the research on estimators cited in the TIME article, the further implication is that the culturally induced shift to a linear number scale is a good thing.
As a street-fighting mathematician, I respectfully disagree. I have been thinking about, teaching, and practicing the art of approximation for almost 20 years: at Caltech, the University of Cambridge, MIT, and Olin College. And I almost always use logarithmic number lines. Halfway between one and nine, I place three.
Here are reasons why a multiplicative, or logarithmic, number line is so useful:
- Many quantities grow by an amount proportional to the amount already present. For example, our raises or cost-of-living adjustments (if any!) are expressed as percentages, say 2.5 percent. This change is a multiplicative change: the new salary is 1.025 times the old salary. In contrast, an additive change would be: “Your annual raise is $2000.” If we happen to get the information in that form, as an absolute amount, we automatically translate it into a fractional change – that is, onto a multiplicative number line.
- Human perception follows the famous Weber–Fechner law: The just-noticeable difference between two stimuli is proportional to the magnitude of the stimuli. As an example, the light-intensity change to which we are sensitive is proportional to the current light intensity. More metaphorically: A $1000 per-head (poll) tax means far more to a migrant laborer than to a hedge-fund partner.
- The world talks to us using signals with a huge range of intensities. For example, our eyes function in starlight and bright sunlight, an intensity range of a factor of 1 billion. Our minds, including our perceptual hardware, manage this vast range partly by using a multiplicative number line. As one piece of that computation, the retina’s rod cells, each one “pixel” of an image, roughly computes the logarithm of light intensity; that is, it places the intensity onto a logarithmic (multiplicative) number line.
Here are typical illumination levels (data from this Wikipedia article) shown on such a number line, with the levels given in scientific notation (where, for example, 102 means 100 and 105 means 100,000):
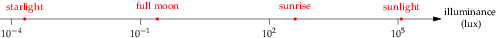 This transformation compresses a huge range of light intensities into a manageable range: It replaces the absolute light intensity with the answer to the question, “How many factors of 10 does the intensity have?” (For those curious about how biochemistry can do such a computation: I also wondered about it, and wrote up an approximate analysis in Chapter 7 of my PhD dissertation.)
This transformation compresses a huge range of light intensities into a manageable range: It replaces the absolute light intensity with the answer to the question, “How many factors of 10 does the intensity have?” (For those curious about how biochemistry can do such a computation: I also wondered about it, and wrote up an approximate analysis in Chapter 7 of my PhD dissertation.) - In everyday life, multiplication is far more useful than addition. For example, suppose you want to estimate, very roughly, an annual budget. Maybe you are a management consultant trying to understand a new industry, or an intelligence agent trying to understand a foreign culture. A budget usually has several important components: for example, salaries and buildings. When finding the total cost, there are three possibilities:
- The salary cost is much larger than the buildings’ cost. In this case, the total cost is roughly just the salary cost.
- The buildings’ cost is much larger than the salary cost. In this case, the total cost is roughly just the buildings cost.
- The salary and buildings’ costs are comparable. Now the total cost is roughly just twice the salary (or buildings) cost.
All we need is multiplication, or scaling, by 2. This idea of scaling is fundamentally different from the idea of repeated joining (how we often think of multiplication, because, sadly, we learn addition before multiplication — but that story is for another time).
Here is another example. If you are like me, after you open your monthly credit-card statement, you might find yourself saying, “$1,500!! How in the
hell did that happen?” To find out, I ignore all the trivial line items, like the pad of paper or the bagel and apple juice when I had no cash on hand. I run my eye over what remains in order to guesstimate two quantities: (1) the cost of a typical large item, and (2) the number of such items. Then I multiply these quantities and check whether the product mostly explains the monthly bill. Almost never do I start adding up the charges. (A far better way to spend time, alas, is to ensure that all the charges are legitimate.)
In short, we need multiplication, not addition. We need multiplicative number lines, not linear number lines. If we start out with logarithmic intuitions — and the evidence is strong that we do — let’s not shed them, let’s amplify them!

Comments